[Coding025] Sort - 拓扑排序
拓扑排序
Get the knowledge flowing and circulating! :)
目录
标题:拓扑排序
在这个例子中,每一门课程对应有向图中的一个顶点,每一个先修关系对应一条有向边(从先修课指向需要先修课的课)。
在数学里,拓扑学(英语:Topology)是一门研究拓扑空间的学科,主要研究空间内,在连续变化下维持不变的性质。在拓扑学里,重要的拓扑性质包括连通性与紧致性。
在计算机科学领域,有向图的拓扑排序(英语:Topological sorting)或拓扑测序(英语:Topological ordering)是对其顶点的一种线性排序,使得对于从顶点
到顶点 的每个有向边 , 在排序中都在 之前。 例如,图形的顶点可以表示要执行的任务,并且边可以表示一个任务必须在另一个任务之前执行的约束;在这个应用中,拓扑排序只是一个有效的任务顺序。
注意:当且仅当图中没有定向环时(即有向无环图),才有可能进行拓扑排序。
任何有向无环图至少有一个拓扑排序。已知有算法可以在线性时间内,构建任何有向无环图的拓扑排序。
在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,才能称为该图的一个拓扑排序:
序列中包含每个顶点,且每个顶点只出现一次;
若A在序列中排在B的前面,则在图中不存在从B到A的路径。
——维基百科
【补充笔记】
Topological Sorting is mainly used for scheduling jobs from the given dependencies among jobs[1].
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列[2]。且该序列必须满足下面两个条件:
每个顶点出现且只出现一次。
若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
拓扑排序实例
| 有向无环图(DAG1) | 有向无环图(DAG2) |
|---|---|
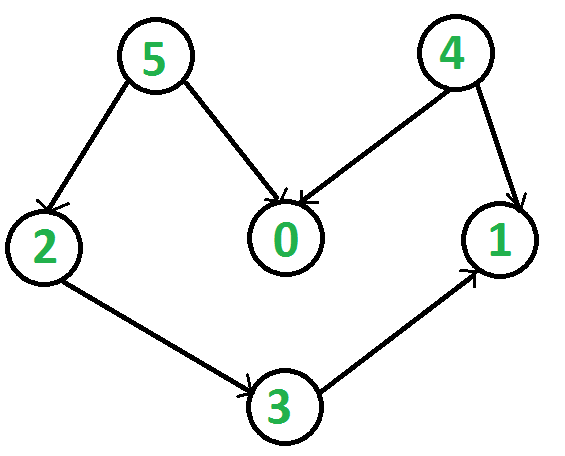 | 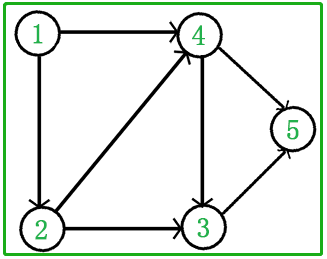 |
| “5 4 2 3 1 0” “4 5 2 3 1 0” 所以,一个有向无环图的拓扑排序并不唯一 | “ 1 2 4 3 5 ” |
有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。 (Topological Sorting for a graph is not possible if the graph is not a DAG.)
一个有向无环图可以有一个或多个拓扑排序序列。(比如DAG1有两个拓扑排序序列,DAG2只有1个)
拓扑排序 V.S 深度优先搜索
拓扑排序不同于DFS,(Topological Sorting vs Depth First Traversal (DFS))。
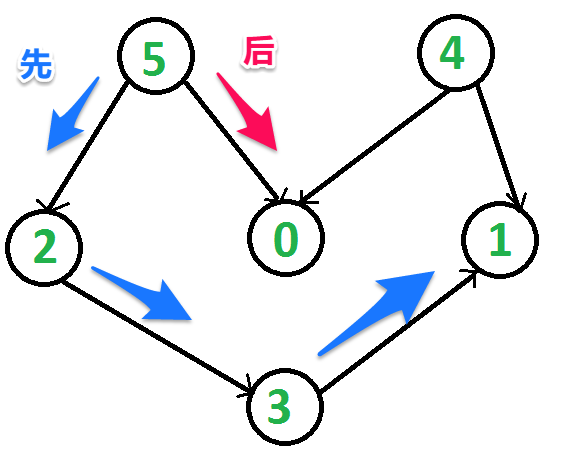
In DFS, we print a vertex and then recursively call DFS for its adjacent vertices.
In topological sorting, we need to print a vertex before its adjacent vertices.
For example
In the given graph DAG1,
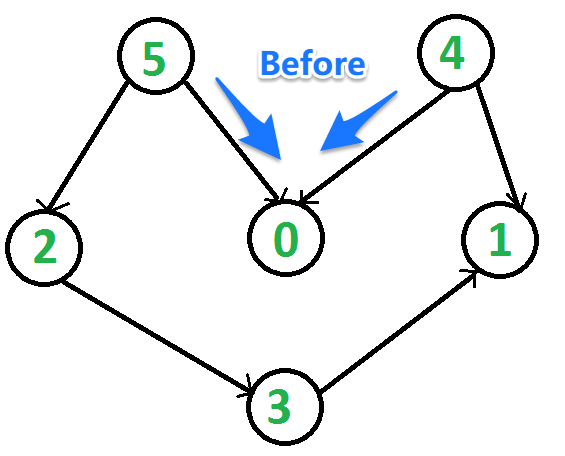
the vertex ‘5’ should be printed before vertex ‘0’,
but unlike DFS, the vertex ‘4’ should also be printed before vertex ‘0’.
A DFS of the shown graph is “5 2 3 1 0 4”, but it is not a topological sorting.
| Topological | DFS |
|---|---|
 |  |
Java语言代码实现
x1import java.util.*;2
3// 有向无环图(DAG)4// 本例用邻接表表示这个有向无环图5class Graph {6
7 // 节点的数量8 private int V;9
10 /*11 * 邻接表12 * 型如: [ 13 * [], 14 * [], 15 * [3], 16 * [1], 17 * [0, 1], 18 * [2, 0] 19 * ] 20 * 双层List: 21 * * 每行的index来表示Vertex的编号 22 * * 每行(单层List)表示对应Vertex的邻接节点23 */24 private ArrayList<ArrayList<Integer>> adj;25
26 // 构造函数27 Graph(int v) {28 29 // 构造一个长度为v的邻接表,可以存放v个节点30 V = v;31
32 // 邻接表及其初始化33 adj = new ArrayList<ArrayList<Integer>>(v);34 35 for (int i = 0; i < v; i++) 36 {37 adj.add(new ArrayList<Integer>());38 }39 }40
41 public int getVertexNumber() 42 {43 return V;44 }45
46 public ArrayList<ArrayList<Integer>> getAdj() 47 {48 return adj;49 }50
51 // 增加一条边,就意味着邻接表里对应的节点的List增加一个节点52 void addEdge(int v, int w) 53 {54 adj.get(v).add(w);55 }56
57 // 递归函数:先push到栈里的是出度为0的节点58 void topologicalSortUtil(int v, boolean visited[], Stack<Integer> stack) 59 {60 visited[v] = true;61 Integer i;62
63 Iterator<Integer> it = adj.get(v).iterator();64 while (it.hasNext()) {65 i = it.next();66 if (!visited[i])67 topologicalSortUtil(i, visited, stack);68 }69
70 stack.push(new Integer(v));71 }72
73 // 拓扑排序的初始化 和 启动程序74 void topologicalSort() 75 {76 Stack<Integer> stack = new Stack<Integer>();77
78 boolean visited[] = new boolean[V];79
80 // 把所有节点都初始化为未遍历状态81 for (int i = 0; i < V; i++) {82 visited[i] = false;83 }84
85 for (int i = 0; i < V; i++) {86 if (visited[i] == false)87 topologicalSortUtil(i, visited, stack);88 }89
90 // 打印栈结果91 while (stack.empty() == false)92 System.out.print(stack.pop() + " ");93 }94}95
96public class Solution {97
98 /**99 * 拓扑排序100 */101 public static void main(String[] args) {102 // TODO Auto-generated method stub103// Scanner input = new Scanner(System.in);104// 105// int n = input.nextInt();106// 107// int[] arr = new int[n];108// 109// for(int i = 0; i < n; i++)110// {111// arr[i] = input.nextInt();112// }113// 114// System.out.println("------------");115// for (int e : arr)116// {117// System.out.print(e + " ");118// }119// System.out.println();120
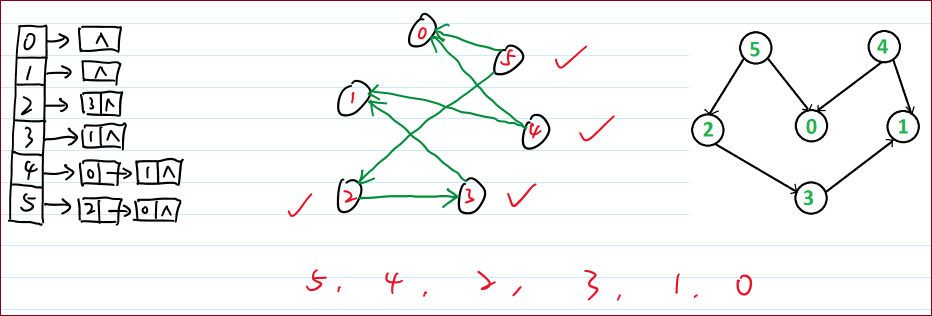
121 Graph g = new Graph(6);122 g.addEdge(5, 2);123 g.addEdge(5, 0);124 g.addEdge(4, 0);125 g.addEdge(4, 1);126 g.addEdge(2, 3);127 g.addEdge(3, 1);128
129 int v;130 ArrayList<ArrayList<Integer>> adj;131
132 v = g.getVertexNumber();133 System.out.println("The Number of Vertex is " + v);134 adj = g.getAdj();135
136 for (int i = 0; i < v; i++) 137 {138 System.out.println(i + "->" + adj.get(i));139 }140
141 System.out.println("Following is a Topological sort of the given graph");142 g.topologicalSort();143
144 }145
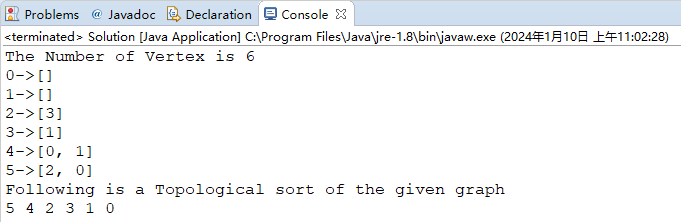
146}运行结果
测试样例:
程序评价
对于有向无环图,可以直接进行操作,输出一个拓扑排序。
【但】对于有向有环图,程序实际上应该报错!但是程序没有!
需要改进!!